Лабораторная работа №2.
Расчет геометрических параметров объекта.
Задача. Склеивание коробки.
Описание задачи.
Имеется квадратный лист картона. Из листа по углам вырезают четыре квадрата и склеивают коробку по сторонам вырезов. Какова должна быть сторона вырезаемого квадрата, чтобы коробка имела наибольшую вместимость? Какого размера надо взять лист, чтобы получить из него коробку с заданным максимальным объемом?
Цель моделирования: определить максимальный объем коробки.
Компьютерная модель:
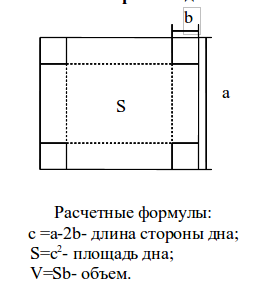
Здесь а- длина стороны картона, b- размер выреза. Первоначальный размер выреза b0=0. Последующие размеры выреза определяются по формуле bi+1=bi+Δb.
Таблица будет содержать три области:
исходные данные;
промежуточные расчеты;
результаты.
Заполните область данных по предложенному образцу. В этой области заданы текстовые исходные параметры a=40см, Δb= 1 см, которые были использованы для расчета длины стороны дна, площади дна и объема коробки при нескольких значениях выреза.
|
А |
В |
|
|
1 |
Задача о склеивании коробки |
|
|
2 |
|
|
|
3 |
Исходные данные |
|
|
4 |
Длина стороны листа |
40 |
|
5 |
Шаг изменения выреза |
1 |
Составьте таблицу расчета по приведенному образцу.
|
|
А |
В |
С |
D |
|
6 |
Расчет |
|
|
|
|
7 |
Промежуточные расчеты |
|
|
|
|
8 |
Размер выреза |
Длина стороны дна |
Площадь дна |
Объем |
|
9 |
Формула 1 |
Формула 3 |
Формула 4 |
Формула 5 |
|
10 |
Формула 2 |
Заполнить вниз |
Заполнить вниз |
Заполнить вниз |
|
11 |
Заполнить вниз |
|
|
|
Введите расчетные формулы по правилам, принятым в среде электронных таблиц:
| Ячейка | Формула | Пояснение |
| А9 | 0 (1) | Начальный размер выреза |
| А10 | =А9+$B$5 (2) | Следующий размер выреза получается прибавлением к предыдущему шага изменения выреза |
| В9 | =$B$4-2*A9 (3) | Длина стороны дна получается вычитанием из заданной стороны листа удвоенного размера выреза |
| С9 | = B9^2 (4) | Площадь дна вычисляется как квадрат длины стороны дна |
| D9 | =C9*A9 (5) | Объем коробки вычисляется как произведение площади дна на размер выреза, который равен высоте коробки. |
Задания:
1. Проследить, как изменяется с увеличением выреза
а) длина стороны дна;
б) площадь дна;
в) объем коробки.
2. Исследовать, как определить наибольший объем коробки и соответствующий вырез.
3. Исследовать, как изменяется наибольший объем коробки и соответствующий вырез при изменении стороны исходного листа.
4. Исследовать, как изменяется наибольший объем коробки и соответствующий вырез, если уменьшить шаг изменения выреза ( например, при b=0.3 см).
5. Подобрать размер картонного листа, из которого можно сделать коробку с заданным наибольшим объемом ( например, 5000 см3).
По результатам экспериментов сформулируйте выводы. Составьте отчет в текстовом процессоре. В отчете отразите этапы моделирования: исходные данные, геометрическую модель, расчетные формулы, результаты экспериментов и выводы.
Пояснения.
Задание 3.
Определите значения наибольшего объема коробки для нескольких значений длины листа. Для этого:
- в ячейку B4 введите новое исходное значение;
- по столбцу В определите допустимый диапазон строк для исследования. При необходимости заполните дополнительное количество строк;
- по столбцу D определите наибольший объем коробки;
- по столбцу А определите размер выреза, соответствующий наибольшему объему.
Результаты экспериментов разместите в ячейках на свободном пространстве электронной таблицы по образцу.
-
Эксперимент
Шаг изменения выреза 1 см
Длина стороны листа
Вырез
Объем
40
60
80
-
Задание 4.
Введите в ячейку новое значение шага изменения выреза (например, 0.3 см). Определите значения наибольшего объема коробки для нескольких значений длины картонного листа. Результаты экспериментов оформите в виде таблицы.
-
Эксперимент
Шаг изменения выреза 0.3 см
Длина стороны листа
Вырез
Объем
40
60
80
-
Задание5. Для подбора размера исходного листа изменяйте значение ячейки и определяйте наибольший объем коробки, пока не добьетесь заданной величины. Результаты разместите в виде таблицы.
-
Эксперимент
Подбор размера листа
Длина стороны листа
Вырез
Объем
3500
5000
12000
-
-
Итоговый вид рабочего листа:
